文汇报/2013 年/5 月/30 日/第 013 版
文汇教育·焦点

“数学是美的。”几乎所有热爱数学的人，都对这一点心领神会。

复旦大学数学科学学院副院长林伟教授最近为了这份“美”，还和一名博士生较了真。博士生交上一篇论文，林伟拿来一瞅，纸面上打印着一排排数学公式，但基本的规范都没遵守，有些变量，该用斜体的都没用。 Continue reading 文汇报 | 被异化的数学正在训练大量“麻袋” →

初中学生通过QQ问了我两个题，其中一题如下“一张桌子由1个桌面，4条桌腿组成，如果1立方米木料可以做方桌的桌面50个或做桌腿300条，现有10立方米木料，用多少立方米的木料做桌面，多少立方米的木料做桌腿，且桌腿和桌面刚好配成方桌？”

我在网上搜索了下，大致有如下几种答案：

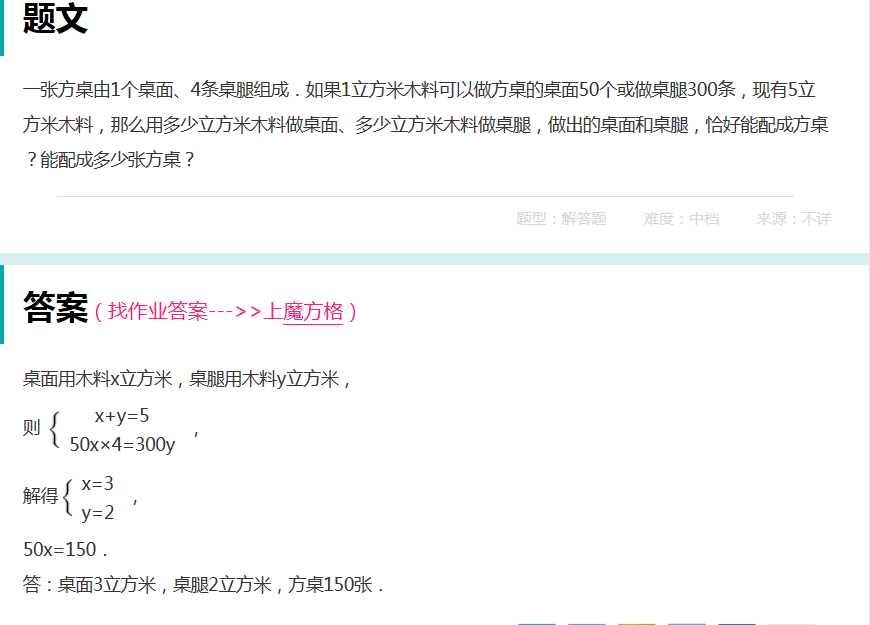（原文链接：http://www.mofangge.com/html/qDetail/02/c0/201310/4yk0c002343330.html）

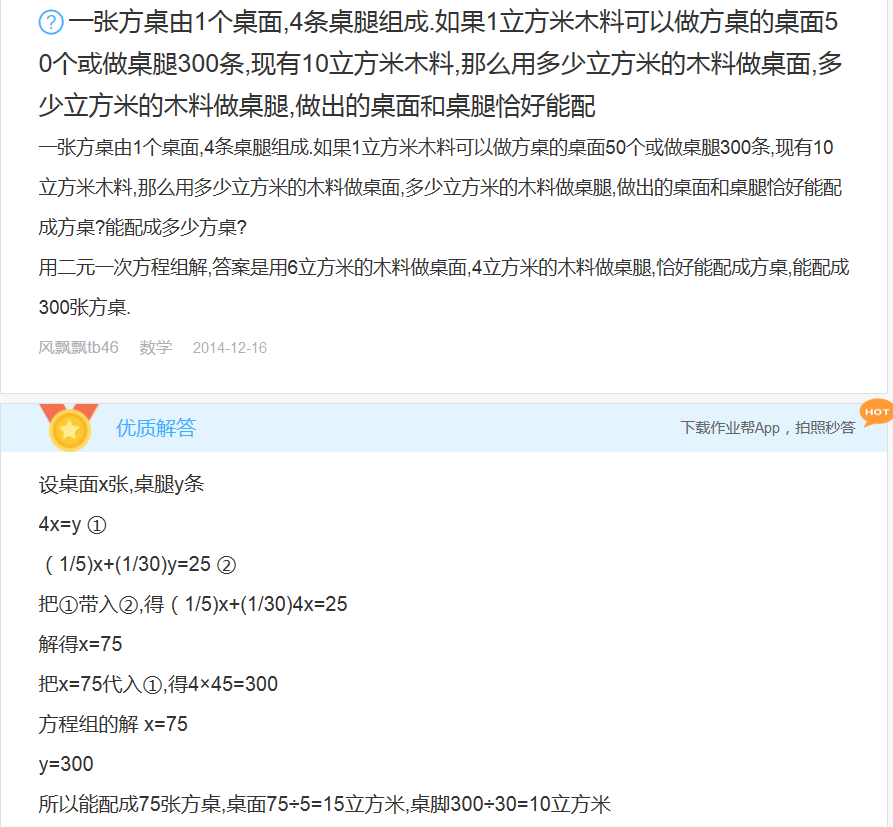(原文链接:http://zuoye.baidu.com/question/dcca1a0325b203b971bcacfb07c98b5c.html)

(原文链接：http://zuoye.baidu.com/question/dcca1a0325b203b971bcacfb07c98b5c.html)

有兴趣的朋友可以验证一下，第一种解答应该是错误的，第二种解答个人认为不知所云何物，第三种解答才是正确的，瞬间感觉百度坑人，误人子弟，有没有？

但是仍然觉得解答过程难以满足学生需求，即不能回答“怎么想到的”，“为什么这么想”，因此我给出了自己的解答过程，力求把思维过程呈现出来，且为学生节省“思维成本”，我把它称作“翻译法”，如图：

学生还问了另一个题，也将解答过程附上：

更正：“翻译法”第一张图有两句话有误，分别是倒数第二行红笔写的“桌面用料”和“桌腿用料”，应该置换位置，特此更正。

图文：阅川

抗击埃博拉病毒、寻找失联的马航MH370飞机——两大发生在去年、困扰全世界的难题，居然成了今年美国数学建模竞赛的试题。此次比赛已于前天正式开锣，很多国内高校报名参赛的数学尖子们大呼，这样的题目真是让人脑洞大开，“简直是要去拯救世界”。

这个周末，大学已经放寒假，校园里一片寂静。但在沪上复旦、上海交大、同济、华东师大等高校，一批数学“高手们”却正经历着最紧张的备战时刻。

用数学建模的方法，解决现实重大问题或难题，对于今年入题的抗击埃博拉病毒、寻找马航失联飞机以及涉及人力资源管理、可持续发展领域的四个问题，不少参赛者感到极具挑战。

“这些问题的开放度很大，没有现成的办法或标准答案，需要我们自己想办法去解决。”复旦大学数学学院三年级本科生张腾是今年的参赛者之一，他和伙伴们这两天正在“头脑风暴”之中，他坦言，“还没有想到满意的解题思路，正在小组讨论呢”。除了建模，比赛还要求参赛者递交一篇文字概要，用通俗的语言介绍一下问题解决的方案。

根据赛制规则，今年美国数学建模竞赛的比赛时间为4天，从美国东部时间2月5日下午8点开始，到2月9日下午8点结束，（即北京时间2月6日上午9点开始，到2月10日上午9点结束）。学生以小组形式参加比赛，每组最多三人。业内人士介绍，今年国内的参赛队伍多达9000多支，以大学生为主，“这两年，美国数学建模竞赛在国内大学非常火爆，这一国际性赛事参赛者中的八九成是中国学生。几乎每一年，都有几支中国高校队伍拿到这一赛事的特等奖。”

华东师范大学数学系教授刘永明介绍，目前，高校里有各种级别的数学建模比赛，这类赛事的鼻祖就是美国数学建模竞赛。从命题思路来看，美国数学建模试题的时效性和开放性非常强，历年来都是如此。“中国的数学建模比赛也已经搞了20多年了，通常情况下，出题者对于问题本身多少有一个参考方案或者答案。而美国的赛事，往往选用一些无解的开放问题，解决方案只有更好，没有最好。”刘永明说，这一国际比赛鼓励学生运用专业领域的知识、学以致用，注重激发学生的创新意识和想法。

据悉，这项赛事的另一特别之处是设有一项禁律：参赛队在竞赛期间不得与队外任何人讨论赛题，连指导老师也在这一禁律之列，队员可利用查询图书资料、互联网上的资料以及求助任何类型的计算机和软件等提出问题解决方案。

刘永明说，大赛对于违规者设有惩戒措施。一旦被查出违规，从参赛队伍的指导老师到参赛单位，都将受到取消本年度参赛资格或下一年度参赛资格的处罚。

美国数学建模比赛部分试题

问题1：根除埃博拉病毒

世界医学协会宣布，已发现新药物可阻止埃博拉病毒传播、治愈不太严重的病患。请建立一个现实的、明智的、有用的模型，除考虑疾病的蔓延、所需药物的数量、可行的输送系统、投放地点、生产疫苗或药物的速度，还可以考虑你的团队认为在根除埃博拉病毒时其他可能重要的因素，把它纳入模型。除了建模，再准备为世界医学协会发表公告准备一份1-2页用非技术性语言写成的信。

问题2：寻找失联飞机

回想一下失联的马航MH370飞机。请建立一个通用的数学模型，帮助“搜索者”制定一个有效的办法，搜索一架从A点飞往B点，已坠毁在诸如大西洋、太平洋、印度洋或南北冰洋等开放水域的失踪飞机。

假设坠落的飞机没有信号。模型需能识别在搜索过程中可能遇到的许多不同类型的飞机，它们经常使用不同的电子传感器。此外，请为航空公司准备一份用非技术性语言写成的1-2页的文字说明，以便他们介绍未来的搜索计划。

母校恩师的论文，不经一师，不长一智